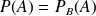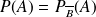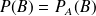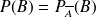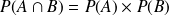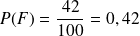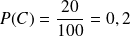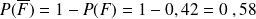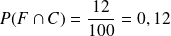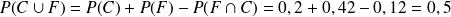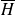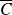Probabilités2
Conditionnement et Indépendance
Avant d'aborder ce chapitre, vous aurez procédé en autonomie à quelques révisions, en particulier sur le chapitre 7 du cours de l'an dernier où on rappelait les premiers éléments du calcul de probabilité et où on replaçait le vocabulaire usuel des probabilités.
Probabilité conditionnelle
Exemple : Enquête au lycée.
Reprenons l'exemple étudié dans le ch7 de l'an dernier et allons un peu plus loin.
On a interrogé 100 étudiants de BTS d'un Lycée, on leur a demandé s'ils étaient allés au cinéma la semaine dernière. Les réponses ont été résumées dans le tableau suivant :
Fille | Garçon | Total | |
|---|---|---|---|
Est allé au cinéma | 12 | 8 | 20 |
N'est pas allé au cinéma | 30 | 50 | 80 |
Total | 42 | 58 | 100 |
On rencontre au hasard l'un des 100 étudiants (tous ont la même chance d'être rencontrés)
On considère les événements :
F : " L'étudiant rencontré est une Fille"
C : " L'étudiant rencontré est allé au cinéma la semaine dernière"
Que désigne l'événement
?
-
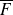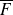: " L'étudiant rencontré n'est pas une fille " ou dit autrement : "l'étudiant rencontré est un garçon".
Que désigne l'événement
?
-
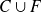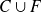: "L'étudiant rencontré est allé au cinéma la semaine dernière OU est une Fille "
Calculer les probabilités :
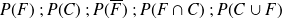
On peut aller un peu plus loin en se posant des question telles que :
Quelle est la probabilité que l'étudiant choisi soit un garçon sachant qu'il est allé au cinéma la semaine dernière ?
Quelle est la probabilité que l'étudiant soit allé au cinéma la semaine dernière sachant que c'est une fille ?
Pour ces deux dernières questions, on remarque que le calcul ne doit plus faire référence à l'ensemble des étudiants interrogés (l'univers), mais chacun de ces calculs prend pour référence un événement particulier. Par exemple, le premier calcul doit clairement se faire dans l'ensemble des étudiants qui sont allés au cinéma la semaine dernière. On parle alors de probabilités conditionnelles.
Ainsi pour répondre , on pourrait utiliser les données du tableau et répondre
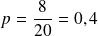pour la première question puis
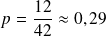pour la deuxième question.
Il y a une façon de calculer plus générale et qui ne nécessite pas d'avoir le tableaux d'effectifs sous les yeux ...
Définition : Probabilité de B sachant A
Définition :
Soient A et B deux événements d'un même univers, de probabilités non-nulles.
La probabilité conditionnelle de B sachant que A est réalisé est notée
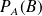et on l'obtient par la formule :
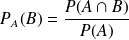
Remarque :
Lors de ce calcul, on peut remarquer qu'on calcule la probabilité de l'événement B non pas dans l'univers tout entier, mais seulement dans l'ensemble que constitue l'événement A.
Complément : Corollaire
A l'aide de la formule de calcul précédente, on peut également calculer la probabilité de l'intersection de deux événements A et B lorsqu'on connaît la probabilité de A et la probabilité de B sachant A.
On a alors
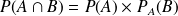
Exemple :
Dans l'exemple précédent, on a calculé
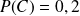(la probabilité que l'étudiant interrogé soit allé au cinéma la semaine dernière) et
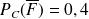(la probabilité que l'étudiant interrogé soit un garçon sachant qu'il est allé au cinéma la semaine dernière) on peut donc en déduire la probabilité que l'étudiant interrogé est un garçon et qu'il est allé au cinéma la semaine dernière,
.
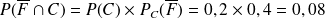Indépendance de deux événements
Événements indépendants
On dit que deux événements sont indépendants lorsque la réalisation de l'un n'influe pas sur la réalisation de l'autre.
Autrement dit, si la réalisation de l'un n'est pas conditionnée à la réalisation de l'autre.
Exemple : Exemple
Dans une PME, on a extrait des informations synthétiques sur les employés qui sont résumées dans le tableau ci-dessous.
Homme (H) | Femme (F) ou (
| Total | |
|---|---|---|---|
Cadre (C) | 12 | 36 | 48 |
Non Cadre (
| 18 | 54 | 72 |
Total | 30 | 90 | 120 |
On tire la fiche d'un employé au hasard, toutes les fiches ont la même probabilité d'être sélectionnées.
La probabilité que ce soit la fiche d'un cadre est
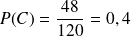
La probabilité que ce soit celle d'un homme est
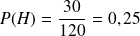
Calculons à présent la probabilité que ce soit la fiche d'un homme sachant que c'est un cadre,
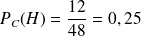
On peut alors remarquer que la probabilité que ce soit la fiche d'un Homme est la même si on calcule dans l'ensemble des fiches ou si l'on regarde juste parmi les cadres.
On dit alors que les événements H et C sont indépendants.
On peut aussi vérifier que
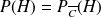
Par suite, on montre également que dans ce cas on a :
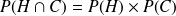
Fondamental : Propriété
Soient A et B deux événements de probabilités non-nulles d'un même univers.
Les propositions suivantes sont toutes équivalentes :
A et B sont deux événements indépendants
Complément : Conséquence dans l'arbre pondéré
Supposons A et B deux événements indépendants, on a l'arbre suivant :
On peut remarquer que dans ce cas où les événements sont indépendants, on lit
et non
sur la branche qui va de A vers B.
