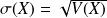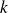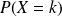Espérance, Variance et Écart type d'une variable aléatoire discrète.
Définition : Loi de probabilité (sur un exemple)
Dans l’exemple précédent, nous avons calculé toutes les probabilités pour les différentes valeurs possibles de
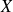 . On peut résumer ces résultats dans un tableau qui décrit la loi de probabilité suivie par la variable aléatoire
. On peut résumer ces résultats dans un tableau qui décrit la loi de probabilité suivie par la variable aléatoire
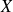 .
.
| 0 | 1 | 2 | 3 |
| 0,343 | 0,441 | 0,189 | 0,027 |
Un rapide calcul permet de vérifier que la somme des probabilités inscrites dans ce tableau est égale à 1. C'est toujours le cas pour une loi de probabilité.
Définition : Espérance (sur un exemple)
Dans notre situation d'étude, on pourrait se demander quelle serait la moyenne des valeurs obtenues pour
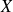 si on faisait un grand nombre de fois le même schéma. Ce résultat est ce qu'on appelle l'Espérance de la variable aléatoire
si on faisait un grand nombre de fois le même schéma. Ce résultat est ce qu'on appelle l'Espérance de la variable aléatoire
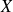 , on la note
, on la note
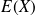 .
.
Ici, on a donc :
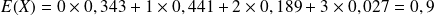
Définition : Espérance, généralisation
Soit
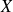 une variable aléatoire discrète qui peut prendre les valeurs
une variable aléatoire discrète qui peut prendre les valeurs

On note
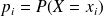 .
.
L’espérance mathématique de la variable aléatoire
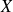 est calculée par la formule :
est calculée par la formule :
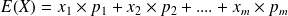
Formule qu'on peut également écrire de la façon suivante :
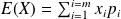
Définition : Variance et écart type
Variance
De même qu'en statistiques, on définit la variance de la variable aléatoire
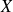 par la formule (avec les mêmes notations que précédemment) :
par la formule (avec les mêmes notations que précédemment) :

Autrement écrit
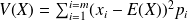
Autre formule (à démontrer à titre d'exercice)

Écart type
Comme en statistiques, l'écart type est défini comme racine carrée de la variance, on a donc :