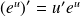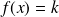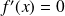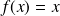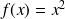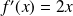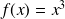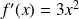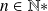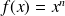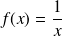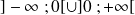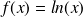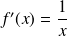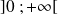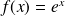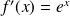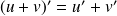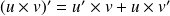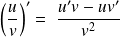Calcul différentiel-fonction dérivée
Définition : Fonction dérivée
Soit
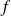 une fonction dérivable sur un intervalle
une fonction dérivable sur un intervalle
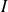 . On appelle fonction dérivée de la fonction
. On appelle fonction dérivée de la fonction
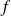 et on note
et on note
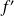 la fonction qui à tout réel
la fonction qui à tout réel
 de
de
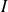 associe le nombre dérivé
associe le nombre dérivé
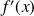 de la fonction
de la fonction
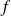 en
en

Fondamental : Dérivées des fonctions de référence
On rappelle que les dérivées des fonctions constante, identité, carré et cube sur
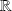 sont connues.
sont connues.
La dérivée de la fonction constante
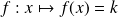 est
est
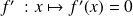 (fonction nulle)
(fonction nulle)La dérivée de la fonction identité
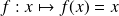 est
est
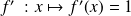 (fonction constante égale à 1)
(fonction constante égale à 1)La dérivée de la fonction carré
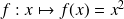 est
est

La dérivée de la fonction cube
 est
est
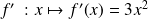
Le tableau suivant rappelle quelques dérivées déjà rencontrées au lycée et est complété par les dérivées des fonctions logarithme népérien et exponentielle.
Il est à connaître parfaitement
Nom de la fonction | Fonction
| Fonction dérivée
| pour tout
|
|---|---|---|---|
Constante (
|
|
|
|
Identité |
|
|
|
Carré |
|
|
|
Cube |
|
|
|
Puissance (
|
|
|
|
Inverse |
|
|
|
Logarithme népérien |
|
|
|
Exponentielle de base e |
|
|
|
Fondamental : Propriétés
Pour déterminer la fonction dérivée d'une fonction construite avec les fonctions de références, le tableau précédent est nécessaire mais pas suffisant ; nous aurons également besoin de quelques propriétés incontournables.
Notations : dans tout ce paragraphe,
 et
et
 désignent deux fonctions définies et dérivables sur un même intervalle
désignent deux fonctions définies et dérivables sur un même intervalle
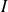
Dérivée d'une somme
"La dérivée d'une somme de deux fonctions est la somme des dérivées des deux fonctions"
Dérivée du produit d'une fonction par une constante
"La dérivée du produit d'une fonction par une constante est le produit de la constante par la dérivée de la fonction"
Remarque, c'est en particulier grâce à ces deux dernières propriétés qu'on calcule aisément les dérivées des fonctions polynômes.
Dérivée du produit de deux fonctions
"attention cette propriété n'est pas
« évidente »
"
Dérivée de l'inverse d'une fonction
"attention cette propriété n'est pas
« évidente »
"
Dérivée du quotient de deux fonctions
"attention cette propriété n'est pas
« évidente »
"
Fondamental : Fonctions "composées"
Fonction dérivée de
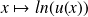
Soit
 une fonction strictement positive et dérivable, de dérivée
une fonction strictement positive et dérivable, de dérivée
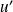 sur un intervalle
sur un intervalle
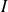 .
.Soit
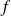 la fonction définie sur
la fonction définie sur
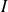 par
par
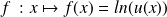
on a :
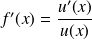
On peut retenir
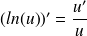
Fonction dérivée de
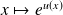
Soit
 une fonction dérivable sur un intervalle
une fonction dérivable sur un intervalle
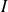 , de dérivée
, de dérivée
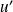 .
.Soit
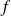 la fonction définie sur
la fonction définie sur
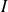 par
par
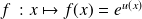
on a :
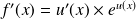
On peut retenir