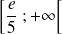Étude des variations d'une fonction
Rappel :
L'étude des variations d'une fonction consiste à préciser sur quels intervalles de l'ensemble de définition la fonction est croissante ou décroissante.
Cette étude préalable permet également d'avoir un aperçu grossier de l'allure de la courbe représentant la fonction. De plus, le tableau de variation qu'on construit à partir de cette étude permet de visualiser des éventuels minimum ou maximum locaux et de répondre à certaines questions du type nombre d'antécédents pour une image donnée.
Nous revoyons ici en détail les théorèmes fondamentaux qui permettent cette étude essentielle.
Fondamental : Théorème Fondamental
Soit
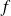, une fonction de dérivée
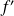sur un intervalle
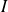de son domaine de dérivabilité.
Si la dérivée
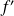est négative sur
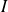, alors la fonction
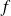est décroissante sur
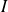.Si la dérivée
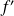est positive sur
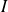, alors la fonction
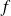est croissante sur
.
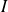Exemple :
Exemple 1
On se propose d'étudier les variations de la fonction
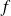définie sur
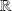par
.
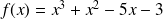Cette fonction est dérivable sur
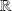et
.
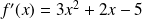D'après le théorème précédent, étudier les variations de
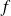revient à étudier le signe de
.
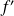(L'étude du signe du trinôme a été revue en première année, chap4)
Signe de
:
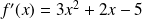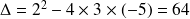est positif, le trinôme
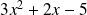admet donc deux racines
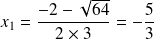et
.
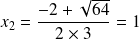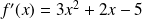est donc positive sur
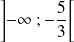et sur
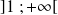
et est négative sur
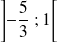
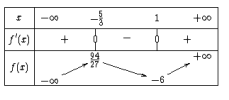
Variation de
:Par conséquent,
est décroissante sur l'intervalle
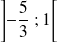
et
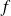est croissante sur chacun des intervalles
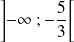et
.
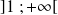Exemple 2
On se propose d'étudier les variations de la fonction
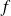définie sur
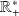par
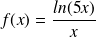
On commence par calculer la dérivée de
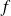, pour tout
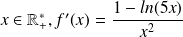
On étudie ensuite le signe de
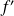en résolvant l' inéquation
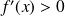(voir chap4 1ere année pour les méthodes de résolution)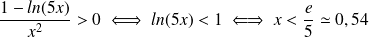
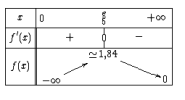
Conclusion
La fonction
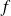est croissante sur l'intervalle
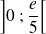et elle est décroissante sur l'intervalle
Complément : Tableau de variation
Les résultats de l'étude des variations d'une fonction peuvent être résumés dans un tableau de variations.
Pour l’exemple 1, on aurait :
Pour l'exemple 2, on aurait :
