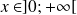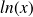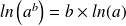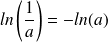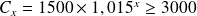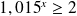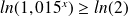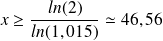Fonction logarithme népérien
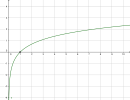
Définition : Définition et représentation graphique
La fonction logarithme népérien est la fonction qui a tout
associe le nombre réel
. Cette fonction est accessible par le clavier de la calculatrice, ou dans un tableur.
Complément : Premières propriétés
La fonction logarithme népérien est strictement croissante sur
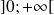
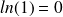
Si
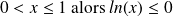
Si
Fondamental : Propriétés algébriques
Propriété fondamentale des fonctions logarithme :
Pour tous nombres réels
et
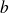strictement positifs,
.
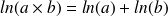Par exemple,
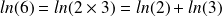
Autres propriétés :
Méthode : Pourquoi et comment utiliser une fonction logarithme.
La recherche algébrique d'une réponse à une question du type "à partir de quel rang le terme général d'une suite géométrique dépasse-t-il une valeur fixée" nécessite l'utilisation d'une fonction logarithme et de ses propriétés.
Par exemple :
Un capital
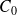de 1500€ est placé sur un livret à intérêts composés rémunéré au taux annuel de 1,5%. Après combien d'années ce capital aura-t-il plus que doublé ?
Le capital disponible chaque année est en progression géométrique comme nous l'avons déjà vu de nombreuses fois.
Appelons
le nombre d'années écoulées depuis le dépôt initial, et
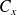le capital disponible à ce moment, avec nos connaissances,
.
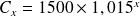Pour répondre à la question nous sommes amenés à résoudre l'inéquation
En divisant par 1500, il vient
Les deux membres de l'inéquation étant positifs et la fonction logarithme népérien étant croissante, on peut l'appliquer aux deux membre de l'inéquation sans en changer le sens ni la nature, on a alors
Comme
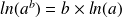, on peut écrire
Et enfin puisque
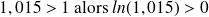et on peut donc diviser les deux membres par
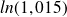sans changer le sens ni la nature de l'inégalité d'où
Conclusion :
Il faut attendre au moins 47 années pour que le capital soit doublé.
