Taux moyen
Taux moyen équivalent
L'idée générale de cette partie est de se donner les moyens de "partager" un taux d'évolution et plusieurs taux d'évolution successifs égaux, qu'on appellera taux moyen équivalent.
Exemple : Évolution trimestrielle
Une start up à vu son chiffre d'affaire progresser de 36% au cours de l'exercice 2014.
Cela représente une évolution trimestrielle moyenne d'environ 8%.
Vérifions ce résultat.
Une année se découpe en 4 trimestres, si l'évolution trimestrielle est de 8%, il faut appliquer cette évolution 4 fois de suite pour avoir l'évolution annuelle. Calculons donc
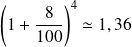qui est le coefficient multiplicateur associé à ces 4 évolutions successives de 8%. Ceci représente bien une évolution globale de 36%.
Comment calculer simplement ce taux moyen d'évolution ? C'est l'objet de cette partie.
Définition : Racine n-ième
Soit
un nombre réel positif et
un nombre entier naturel non-nul.
L'équation
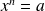admet une unique solution positive, le nombre
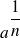, parfois noté
.
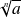Ce nombre s'appelle la racine n-ième de
.
Exemple :
2 est la racine cubique de 8, en effet,
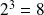, ou encore
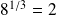.La racine cinquième de 1024 est 4, en effet,
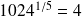
La racine quatrième de 1,36 est environ 1,08
Fondamental : Propriété
Soit
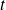le taux d'évolution global d'une quantité sur une certaine période,
soit
le nombre de subdivisions de la période en question.
Le taux moyen équivalent
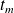pour chaque subdivision de la période, vérifie l'égalité :
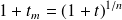
Autrement dit, le coefficient multiplicateur associé au taux moyen équivalent pour chacune des
subdivisions de la période est la racine n-ième du coefficient multiplicateur associé au taux d'évolution global de la période.
Remarque : Subdivisions usuelles
Lorsqu'on divise une année on a :
2 subdivisions c'est 2 semestres
4 subdivisions c'est 4 trimestres
12 subdivisions c'est 12 mois
