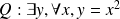Calcul des prédicats
Définition : Prédicat
Dans la partie "proposition", j'annonçais que l'énoncé "
" n'était pas une proposition en tant que tel mais qu'en ajoutant une information sur la variable
on pouvait en faire une proposition.
Par exemple en écrivant : Il existe un réel
tel que
on obtient une proposition Vraie.
Par exemple en écrivant : Pour tout nombre réel
,
on obtient une proposition Fausse.
On dit alors que "
" est un prédicat à une variable, on peut le noter
Exemple : Quelques exemples de prédicats.
"Le chat est gris" est un prédicat. "Le chat de ma voisine est gris" est une proposition.
"
" est un prédicat. "pour
" est une proposition (Fausse)
Définition : Quantificateurs
Dans la définition précédente, l'information supplémentaire sur la variable
était quantifiéede deux façons différentes.
« Il existe un réel
signifie "Il existe au moins un réel
»
". La locution "Il existe" s'appelle le quantificateur existentiel, on le note
et on le lit "il existe au moins " ou encore "pour au moins un"La proposition Il existe un réel
tel que
s'écrit en langage mathématique :« Pour tout nombre réel
utilise le quantificateur universel, qu'on note
»
et qu'on lit "quelque soit" ou encore "pour tout"La proposition Pour tout nombre réel
,
s'écrit en langage mathématique :
Attention : Ordre des quantificateurs
Soient
et
deux nombres réels, soit le prédicat à deux variables
Considérons les propositions :
signifie "pour tout nombre réel
, il existe un nombre réel
tel que
", c'est une proposition vraie car tout nombre réel possède un carré.
signifie "il existe au moins un nombre réel
égal à tous les carrés des nombres réel", c'est évidement une proposition fausse.
Conclusion : Attention à l'ordre lors de l'écriture des quantificateurs.
Complément : Négation des propositions quantifiées.
Prenons l'exemple de la proposition vraie
la négation de cette proposition est la proposition fausse
.
Prenons l'exemple de la proposition fausse
la négation de cette proposition est la proposition vraie
.
Et de façon tout à fait générale,
soit
un prédicat,
"La négation de pour tout
on a
est Il existe un
tel que
".
"La négation de il existe
tel que
est pour tout
on a
".
Méthode : Méthode
Pour montrer qu'une proposition quantifiée par
est vraie, il suffit de présenter un exemple.
Par exemple :
est Vrai car en choisissant
on a :
Pour montrer qu'une proposition quantifiée par
est fausse, il suffit de présenter un contre exemple. (c'est à dire un exemple tel que la négation de la proposition soit vraie)
Par exemple : pour montrer que
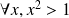est Faux, on utilise que
est Vrai en choisissant par exemple
.
