Suites numériques - généralités
Suites numériques
L'étude des suites numériques est essentielle pour étudier des phénomènes et des modèles discrets, les applications sont nombreuses en mathématiques financières. Nous porterons particulièrement notre attention sur les suites arithmétiques (qui modélisent par exemple des placements à intérêts simples) et les suites géométriques (qui modélisent par exemple des placements à intérêts composés).
Définition : Suite numérique
Une suite numérique peut être vue comme une fonction de
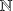(ou d'une partie de
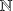) dans
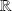, c'est à dire qu'à tout entier naturel
on fait correspondre un nombre réel qu'on note
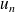et qu'on appelle le terme de rang
de la suite
.
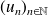Complément : Modes de génération d'une suite.
1. Suite définie explicitement (par une fonction)
Dans ce cas, chaque terme
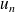de la suite est défini directement en fonction de
.
Par exemple : pour tout
,
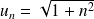
Ici, on a :
;
;
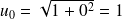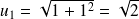Exercice : de la même façon, calculer
,
,
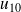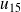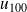
2. Suite définie par une relation de récurrence.
Dans ce cas, on définit un terme de la suite en utilisant le terme précédent. Il faut également préciser le terme initial de la suite sans quoi aucun autre terme ne peut être calculé.
Exemple : On considère la suite
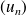définie par :
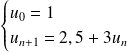
Notez bien qu pour pouvoir calculer
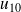, il faudra d'abord calculer
