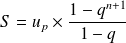Suites géométriques
Définition : Définition
On dit d'une suite numérique qu'elle est géométrique lorsque le quotient de deux termes consécutifs est un nombre constant. Ce nombre s'appelle alors la raison de la suite.
Soit
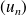une suite numérique,
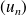est une suite géométrique si et seulement si pour tout
on a :
.
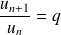Fondamental : Terme général d'une suite géométrique.
Soit
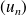une suite géométrique de raison
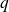et de premier terme
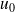. Le terme général
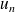de la suite
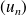peut être défini :
par récurrence :
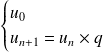
explicitement (par une fonction) : Pour tout
,
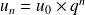
Fondamental : Sens de variation d'une suite géométrique
Soit
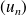une suite géométrique de raison
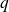
La suite
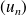est :
croissante si et seulement si
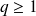
décroissante si et seulement si
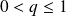
Complément : Somme de termes consécutifs d'une suite géométrique.
Pour évaluer une somme
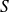de termes consécutifs d'une suite géométrique de raison
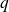, on calcule :
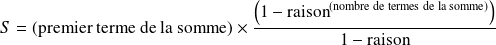
Soit
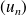une suite géométrique de raison
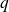, soit
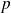et
deux nombres entiers naturels.
Considérons la somme
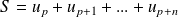
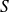est la somme de
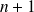termes consécutifs de la suite
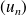
On a donc
