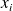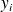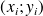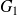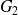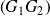Statistiques à deux variables
Définition
On définit une série statistique à deux variables lorsqu'on étudie deux caractères d'une même population.
Par exemple : Dans une entreprise, on relève pour les six derniers mois le nombre de commandes
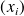 et le chiffre d'affaires réalisé
et le chiffre d'affaires réalisé
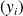 . La donnée des couples
. La donnée des couples
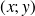 constitue une série à deux variables.
constitue une série à deux variables.
Nombre de commandes
| 6 400 | 8 350 | 9 125 | 9 600 | 10 050 | 12 000 |
Chiffre d'affaires
| 250 | 320 | 335 | 350 | 370 | 400 |
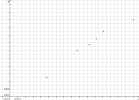
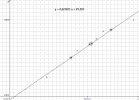
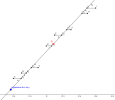
Nuage de points
Point moyen
On appelle point moyen du nuage le point G qui a pour coordonnées
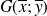
Dans notre exemple :
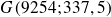
Droite d'ajustement
Lorsque le nuage de points s'y prête, c'est à dire lorsque le nuage semble s'étirer autour d'une droite, on peut chercher à définir une droite qui passe "au plus près" des points du nuage.
Il existe différentes droites d'ajustement affine, nous utiliserons essentiellement la droite de régression de y en x donnée par la calculatrice. L'équation de cette droite est calculée par la méthode dite des moindres carrés.
Deux exemples d'ajustement affine
Droite de régression de y en x
 Méthode des moindres carrés. (voir le fichier droite-regression.ggb dans votre dossier /devoirs/ sur le réseau)
Méthode des moindres carrés. (voir le fichier droite-regression.ggb dans votre dossier /devoirs/ sur le réseau)
A, B, C, D, E, F, H et I sont les points du nuage pour lesquels on cherche la droite de régression de y en x.
On trace une droite passant par le point moyen G, et on définit les points
 ,
,
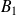 , etc... qui appartiennent à cette droite et qui ont respectivement les mêmes abscisses que les points A, B, etc ...
, etc... qui appartiennent à cette droite et qui ont respectivement les mêmes abscisses que les points A, B, etc ...
On cherche la pente de la droite qui passe par G et qui minimise
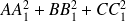 + ...
+ ...
L'équation de cette droite, sous la forme
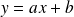 nous sera donnée par la machine à calculer ou le tableur.
nous sera donnée par la machine à calculer ou le tableur.
Droite de régression de x en y
En raisonnant de manière analogue à ce qui précède mais en cherchant à présent à minimiser les carrés des résidus mesurés "en x", on définit une deuxième droite de régression pour laquelle on donne une équation sous la forme
 .
.
Les nombres
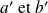 sont obtenus à la calculatrice à partir du travail précédent en échangeant simplement le rôle des variables
sont obtenus à la calculatrice à partir du travail précédent en échangeant simplement le rôle des variables
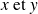 .
.
Coefficient de corrélation linéaire
Le coefficient de corrélation
 donné par la calculatrice lors de l'affichage de l'équation d'une droite de régression linéaire donne une information sur la "qualité" de l'ajustement ou encore sur le bien-fondé du choix d'un ajustement par la méthode des moindres carrés.
donné par la calculatrice lors de l'affichage de l'équation d'une droite de régression linéaire donne une information sur la "qualité" de l'ajustement ou encore sur le bien-fondé du choix d'un ajustement par la méthode des moindres carrés.
Quelques propriétés du coefficient de corrélation r
Soient
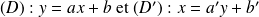 les droites de régression d'une série statistique à deux variables.
les droites de régression d'une série statistique à deux variables.
 est un nombre compris entre -1 et 1
est un nombre compris entre -1 et 1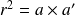
Si
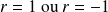 alors l'ajustement est "parfait", les droites
alors l'ajustement est "parfait", les droites
 sont confondues.
sont confondues.