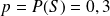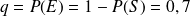Schéma de Bernoulli
Définition : 1) Epreuve de Bernoulli
On appelle épreuve de Bernoulli une expérience aléatoire qui n'a que deux issues, Succès (S) ou Echec (E).
La probabilité d'un succès est notée
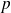, on a donc
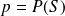
La probabilité d'un échec est notée
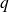, on a donc
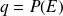
Par suite, étant donné que les événements S et E sont des événements contraires, on a :
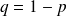
Exemple : Exemple 1
Manu est commercial pour une entreprise qui commercialise des systèmes et services de télé-surveillance. Il démarche ses clients à domicile et établit des devis. Il estime que la probabilité qu'un client accepte un devis est de 0,3.
Pour chaque client démarché, on peut définir les événements S : "Le client accepte le devis" et E : "Le client n'accepte pas le devis" et on a :
Cette situation est une épreuve de Bernoulli.
Définition : 2) Schéma de Bernoulli
On parle de schéma de Bernoulli lorsqu'on répète, de manière indépendante, une épreuve de Bernoulli un nombre donné de fois. On schéma de Bernoulli se représente usuellement par un arbre (binaire) : |  |
Exemple : Exemple 2
Manu prend au hasard les devis de trois clients. Le choix pour un client d'accepter ou non le devis ne dépend pas de la décision des autres clients, ainsi on peut considérer que prendre trois devis revient à répéter 3 fois la même expérience aléatoire (épreuve de Bernoulli), de façon indépendante, chacune de ces épreuve ayant la probabilité de succès
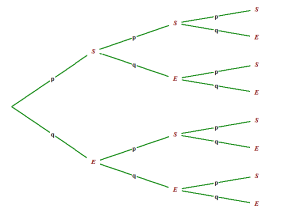
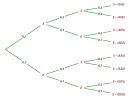
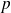. On peut considérer l'arbre suivant, avec en bouts de branches le mot formé par les trois expériences.
On lit sur cet arbre que la probabilité d'obtenir exactement 1 devis accepté sur les trois correspond aux trois issues incompatibles S-E-E ; E-S-E et E-E-S.
Chacune de ces issues a pour probabilité
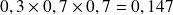donc la probabilité d'obtenir exactement un devis accepté sur les trois choisis est égale à
.
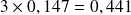Définition : Variable aléatoire associée à un schéma de Bernoulli
On rappelle que la répétition de
épreuves de Bernoulli de probabilités
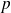, identiques et indépendantes constitue un schéma de Bernoulli.
On définit la variable aléatoire
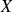associée aux nombres de succès du schéma de Bernoulli :
-
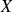peut prendre toutes les valeurs entières
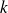de
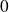à
. 
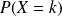est la probabilité d'obtenir exactement
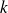succès à l'issue du schéma.
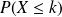est la probabilité d'obtenir au plus
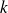succès.
Exemple :
Dans l'exemple précédent, on peut définir la variable aléatoire
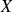qui compte le nombre de devis acceptés lorsqu'on en choisit trois au hasard, et on a :
.
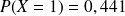