Loi uniforme
Exemple de loi à dansité : loi Uniforme
Intentions :
La loi uniforme permet de modéliser une situation "d'équiprobabilité" dans le cas d'une variable aléatoire continue.
Exemple : Exemple : Passage du bus
Sur la ligne 2 de la TCAT, un bus passe toutes les 20 minutes. Je me trouve rue de la Paix, en direction du centre ville, je m’arrête et j'attends le passage d'un bus.
J'appelle
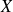la variable aléatoire qui prend comme valeur mon temps d'attente en minutes.
Il est clair que
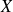peut prendre ses valeurs continuement dans l'intervalle
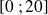, il me semble également assez clair que la probabilité que j'attende exactement 5 min ou bien 10,7 min ou n'importe quelle autre "valeur isolée" est nulle.
Pour autant, la somme des probabilités doit être égale à 1, c'est à dire que la probabilité que mon temps d'attente soit compris entre O et 20 min est égale à 1, ce qu'on peut écrire mathématiquement :
.
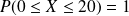On peut observer ceci graphiquement , avec la fonction
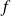ainsi définie ;
Si
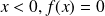;Si
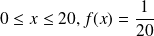;Si
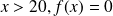
La probabilité que j'attende plus de 20 min est nulle :
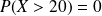;La probabilité que j'attende entre 0 et 20 min est égale à 1 :
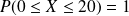; C'est l'aire du grand rectangle hachuré.La probabilité que j'attende entre 10 et 14 min est de
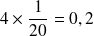, c'est l'aire du rectangle "damier". Cela s'explique intuitivement par le fait qu'entre 10 et 14 min il y a 4 minutes soit
de 20 minutes et que le bus peut passer n'importe quand, de façon "équiprobable" dans l'intervalle des 20 min.
La fonction
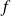définie ci-dessus s'appelle la fonction de densité de la loi uniforme sur l'intervalle
.
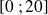Définition : Généralisation
Soit
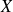une variable aléatoire continue, associée à toute valeur d'un intervalle
.
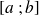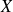suit la loi uniforme telle que :
pour tout nombre réel
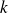de l'intervalle
,
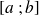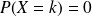et
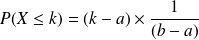;pour tous nombres réels
et
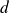de l'intervalle
,
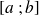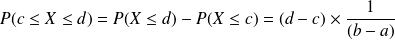;la fonction de densité de cette loi uniforme est la fonction
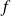définie par :pour tout
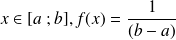
pour tout
Complément : Espérance, Variance et Écart type.
Les résultats suivants sont admis, nous en vérifierons la cohérence en simulant une loi uniforme avec un tableur en Travaux Pratiques.
Pour la loi uniforme sur
,
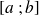L'Espérance est :
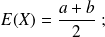
La Variance est :
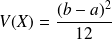;L’Écart type est :
.
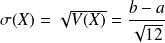