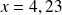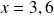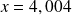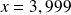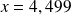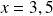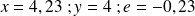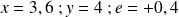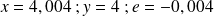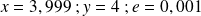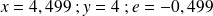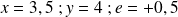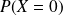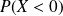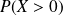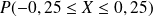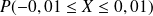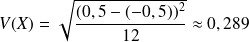Loi Uniforme : Exercice 2
Problème
Soit
un nombre réel et
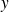l'arrondi à l'unité de
. L'approximation de
par
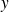est faite avec une "erreur"
.
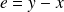L'objectif de ce problème est d'observer et de mesurer d'un point de vue de probabilités l'erreur faite lorsqu'on arrondit un nombre à l'unité.
Question
Question 1 :
Déterminer
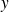et
pour les valeurs suivante de
:
On note
la variable aléatoire qui, à tout nombre réel tiré au hasard, associe l'erreur faite lors de l'arrondi à l'unité.
On admet que
suit la loi uniforme sur l'intervalle
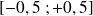
Question
Question 2 :
Donner la fonction densité de
.
Par définition, la fonction densité de
est la fonction
définie par :
Pour tout
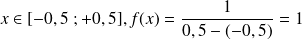
Pour tout
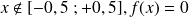
Question
Question 3 :
Déterminer les probabilités :
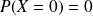, comme pour toute probabilité d'une valeur isolée d'une variable aléatoire continue.
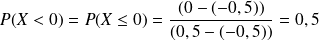. C'est à dire que la probabilité que le nombre soit arrondi à l'entier inférieur est égale à 0,5
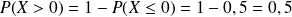, pour faire ce calcul, on utilise le fait que
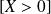est l'événement contraire de
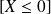
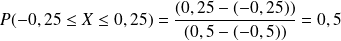
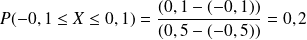
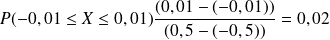
Remarque :
Ces résultats sont bien cohérents avec l'idée intuitive qu'on peut se faire le l'arrondi à l'unité d'un nombre .
Question
Question 4 :
Déterminer l'espérance de
.
Donner une interprétation de ce résultat et dire pourquoi il était prévisible.
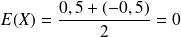
L'espérance de
est la valeur moyenne de l'erreur faite lorsqu'on arrondit les nombres à l'unité,
Il était naturellement prévisible d'obtenir 0, car lorsqu'on arrondit un grand nombre de valeurs à l'unité on cherche justement à faire en sorte que les erreurs dues à l'arrondi se "compensent" pour s'annuler en moyenne.
