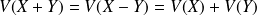Variables aléatoires indépendantes, Théorème de la Limite Centrée
Fondamental : Variables Aléatoires Indépendantes
Espérance et Variance
Soient
et
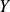deux variables aléatoires, liées à une même situation, d'espérance
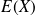et
et de variance
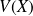et
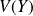, soient
et
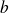deux nombres réels.
On admet les résultats suivants :
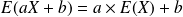
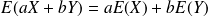et en particulier
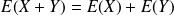et
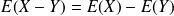
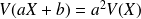
Propriété :
X et Y sont indépendantes si et seulement si pour tous réels
et
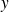on a
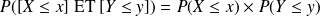
Dans ce cas on a également :
Fondamental : Théorème de la limite centrée
Considérons
variables aléatoires
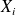indépendantes et suivant toutes la même loi d'espérance
et d'écart type
.
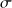On observe la variable aléatoire
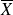, moyenne des
.
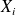Pour
assez grand, la variable aléatoire
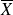suit approximativement la loi normale
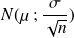d'espérance
et d'écart type
