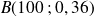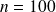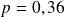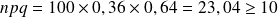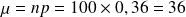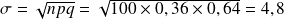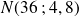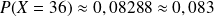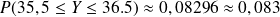Approximation d'une loi binomiale par une loi normale
Fondamental : Approximation dune loi binomiale par une loi normale
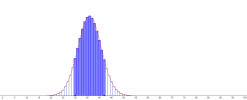
Sous certaines hypothèses, il est possible d'approcher une loi binomiale
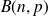 par une loi normale dont les paramètres sont l'espérance et l'écart type de la loi binomiale.
par une loi normale dont les paramètres sont l'espérance et l'écart type de la loi binomiale.
Théorème :
Soit
 une variable aléatoire continue suivant la loi binomiale
une variable aléatoire continue suivant la loi binomiale
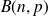
Si
 est "assez grand"
est "assez grand"
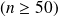
Si
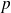 est ni trop petit (proche de 0) ni trop grand (proche de 1) et
est ni trop petit (proche de 0) ni trop grand (proche de 1) et
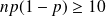
Alors on peut approcher la loi binomiale
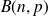 par
par
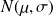 avec
avec
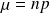 et
et
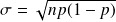
Correction de continuité :
Étant donné que la variable aléatoire
 suit une loi binomiale, elle prend des valeurs entières
suit une loi binomiale, elle prend des valeurs entières
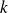 , il est nécessaire de faire une correction de continuité lorsqu'on procède à l'approximation par une loi uniforme.
, il est nécessaire de faire une correction de continuité lorsqu'on procède à l'approximation par une loi uniforme.
Pour cela , l'événement
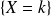 de la loi binomiale est remplacé par l'événement
de la loi binomiale est remplacé par l'événement
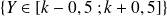 de la loi normale.
de la loi normale.